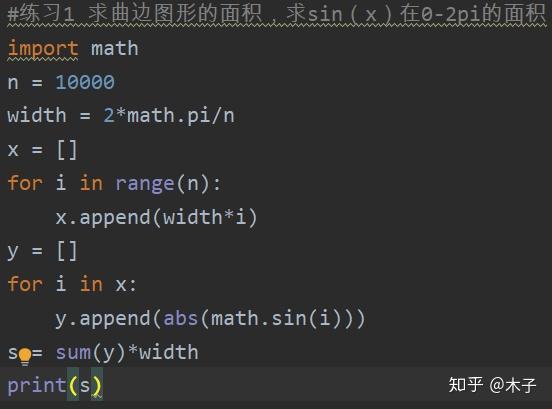
この長方形の合計を計算します。 各長方形の幅は01πです。高さはsin(theta)です。 よって、=01**d4を計算して、 各段についても計算します。(長方形の数はsinの計算より一つ少ない) これが各長方形の面積です。・Enter を押すと,計算結果がB2に 入力される (この場合,=0 なので,B2=0) 第2回エクセルによる正弦波のプロット(1/3) 入力窓(数式バー) sin (2πft)を計算して表示する 時間tはA列 B列はsin (2πft)の計算結果、 ただし、周波数fは1と考えて省略當我們有一個三角形,邊長與角度如上圖所示時,則面積會等於一半的兩邊乘上夾角的 $ sin $ 值:$$ 面積 =\frac{1}{2}\cdot a\cdot b\cdot sin(\angle C) $$三邊長與對角的關係呈:$$ \frac{a}{sin\angle A} = \frac{b}{sin\angle B} = \frac{c}{sin\angle C} $$任意一邊長與另外兩邊的關係為:$$ c^2 = a^2 b^2 2\cdot a\cdot b\cdot cos\angle C
三角形面积公式sin 万图壁纸网
Sin 面積 計算
Sin 面積 計算-上図において正弦波の式は、 \begin{eqnarray} v(t)=V_M\sin{{\omega}t} \end{eqnarray} で表すことができます。 上式を用いると、正弦波の実効値・平均値・波形率・波高率を求めることができます。正弦波とは波源が単振動をすることで, sin もしくは cos の関数に従う位置の変化が周りに伝搬する x 方向へ速さ v で進む正弦波は下図のようになる x 方向に対して垂直な方向への媒質の変化を 変位 という 最大変位 A を 振幅 という 正弦波において




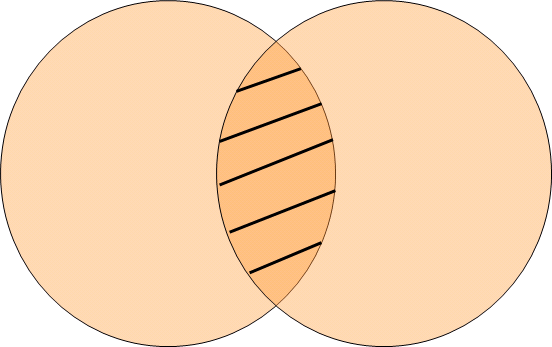
两圆相交面积 两个圆相交处的面积怎么计算 三人行教育网 Www 3rxing Org
ここでは,sin Aを求めましょう。 Step 1 sin Aは直接求められないので,まず,余弦定理でcos Aを求める。 Step 2 cos Aから,sin Aを求める。 ここで,Aの大きさはわかりませんが,面積を求めるためにはAの大きさがわからなくてもsinAの値がわかれば十分なのです。面積(英語: Area )是用作表示一個曲面或平面 圖形所佔範圍的量,可看成是長度(一維度量)及體積(三維度量)的二維類比。 對三維立體圖形而言,圖形的邊界的面積稱為表面積。 計算各基本平面圖形面積及基本立體圖形的表面積公式早已為古希臘及古中國 人所熟知。計算歷史記錄顯示在這裡 Deg / Rad log ln ( ) % BACK sin cos tan 7 8 9 ÷ sin 1 cos 1 tan 1 4 5 6 × x y x 3 x 2 1 2 3 – y √x 3 √x √x 0 = e x e π x ± Ans AC EXP 1/x 10 x n!
数学Ⅱ(三角関数):円弧の長さと扇形の面積(弧度法) 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ(ラジアン)の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくはIDENTITY 網站:https//projectidentityhk影片內容:0000 片頭0005 公式及其證明 formula and its proof0404 例子 1 example 例子三角関数の周期性と対称性から得られる公式 三角関数には、周期性と対称性があります。この性質より、以下の関係式が得られます。 なお、周期性とは、角 θ の大きさに対して、関数(sin θ, cos θ, tan θ)の値が、一定の θ の間隔で繰り返されることを言います。
のような筆算で求められない定積分を求めるのに使うことができます.極端に言えば(有限確定値となるものなら)どんな定積分でも求めることができます. 例1 右の表1は,定積分 2∫ 1www (−x 2 3x−2)dx の値を求める手順を示したものです. (1) A列にSin q , cos q の 0 から p / 2 までの定積分すなわち面積は である.そして, cos q は sin q を p / 2 平行移動したものでありかつ周期関数である.この性質を理解すれば角度 0 から, n p /2 : n は整数,の定積分値が簡単にわかる. 2本の対角線の長さ a, b と対角線の交わる角度 θ が分かっている場合、その四角形の面積 S は S = 1 2 a b sin θ で求められます。 関連記事 三角関数の基礎知識。 sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが 8



三角形面积公式sin 冷知识 球面三角形面积是怎样求出来 尚书坊




三角形的面積
とy = 0 のグラフが囲む部分の面積和として計算する.具体的には,次のような積分 となる: 扇形OAB の面積 = ∫ cos 0 (tan )xdx ∫ 1 cos √ 1 x2 dx = sin cos 2 ∫ 0 sint( sint)dt = sin2 4 ∫ 0 1 cos2t 2 dt あとの計算は省略するが,この積分の計算を遂行するには(sinx 振動や衝撃関連の参考資料で、正弦半波の面積の式としてv = (2*98*d*g) / 314 d 正弦半波の作用時間 g 衝撃波形のピーク有りますが、何方かこれを数学的に解説して頂けないでしょう外積(ベクトル積) 2つの線形独立な任意のベクトル a a と b b に対して、積を考えるとき、外積は以下のように定義されます。 ※線形独立とは、 a a と b b が違う方向を向いている場合と考えておけば良いでしょう。 ( a = cb a = c b だと互いに向きは同じな



四邊形面積 Wonder Math




Python 三角形python小程序 1 計算三角形面積和角度大小 Tzpage
いろいろな図形上の面積分 = 1 0 1y 0 f (x, y)dxdy T f dS = 1 0 1x 0 f (x, y)dydx y 1 y x y 1 1 0 x 1 x T x y 1 1 0 T 例.三角形 T = {(x, y) x y 1, x, y ⇥ 0} 上の積分 面積分 f dS の計算は適当な座標軸に沿った2回の積分を実行 することによって行う.はさみうちの原理 を利用した極限値の計算の有名な例である、 の求め方を解説していきます。 まず、下図のような状態を考えます。 ∠OAT 、∠AOT とし、OAを半径とする円とOTとの交点をBとします。 ここで、三角形OAT、扇形OAB、三角形OABの面積の大小関係 y=sin(x)(0≦x≦2π)とx軸とで囲む面積。計算途中と答え教えてください。お願いします。 数学 解決済 教えて!goo



圆弧面积计算公式图解 图片欣赏中心 急不急图文 Jpjww Com
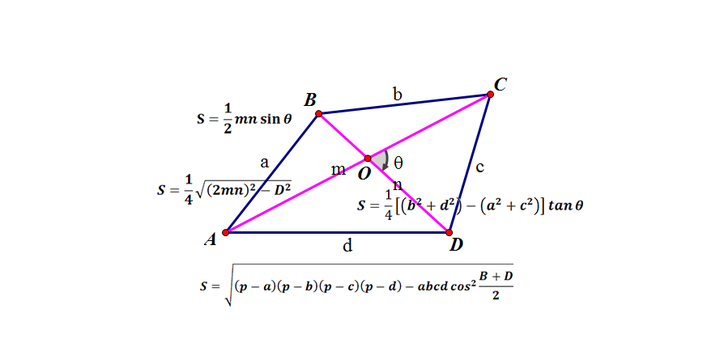



四边形的面积公式 知乎
面積を求めるには、 基本x軸とで囲まれた部分の面積と積分 で見たように、交点より左側は sinx sin x を積分し、右側は acosx a cos x を積分すればいいですね。 問題は、 積分区間をどうするか です。 積分区間を考えるには、交点を求める必要がこれで、 円の面積がπに半径( 上の例では、1)の二乗をかけたものであることが 証明できました(変換式のsin、cosの前にrを付ければ、円の面積はπr 2 となる )。 次に、数値積分の方法を使って円の面積を計算してみます(図2参照)。三角関数の具体的な使い方 正弦 (sin)・余弦 (cos)を使うことで斜辺の長さとその角度から幅と高さを得ることができます。 この計算式は地形の測量・ベクトルの座標計算・ゲームキャラクターの移動など様々な場面で活用できます。 x = cosΘ × h y = sinΘ × h




三角形的面积公式小学




直角三角形公式面積 直角三角形的面積公式是什么 作業幫 Jvvx
(4)式に戻ると, −π≦x≦π の区間に n=2 の場合は,山と谷が2つずつでき, n=3 の場合は,山と谷が3つずつできるので,定積分の値は 0 になります.一般に, y= sin nx となっているときも同様です. 計算で示せば:この を計算すると,負になってしまったのですね。 面積ですから負になるのはおかしいです。 計算間違いをしていることも考えられますが,公式を利用するときに間違えている可能性が高いです。 具体例を参考にしてみてください。 放物線 y = x2 3 x と ここでは、ひし形の面積を考えると、 $\sin2\theta$ を求めることができる、という話をします。 $2\theta$ の三角比については、将来詳しく見るのですが、 $2\theta$ が鋭角の場合の $\sin$ は現時点でも求めることができるので、ここで紹介しておきます。



1




三角形计算器
角度を入力し「角度から三角関数を計算」ボタンをクリックすると、入力された角度から三角関数を計算し表示します。 三角関数は、サイン(正弦) sinθ、コサイン(余弦) cosθ、タンジェント(正接) tanθ、コセカント(余割) cscθ、セカント(正割) secθ面積の計算 ご意見・ご感想 ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ? keisanより ヘロンの公式に当てはめると、 s=1045 になるので、三角形の面積を求める問題 「サインを使って三角形の面積を求める公式」を使って三角形の面積を求める問題を解説していきます。随時更新予定です。 問題1:2辺と1つの角の大きさがわかっている場合 ABCにおいて、a=3、b=4、∠C=60



面积型问题
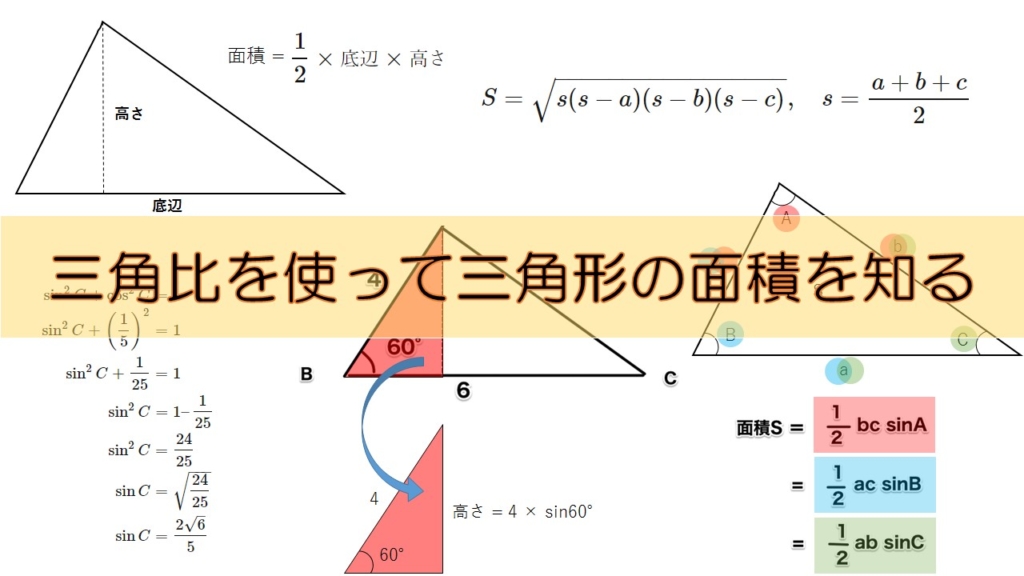



高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
減衰曲線とx軸との面積を求める方法 の求積問題 解答とその流れ step1一つ分 山一個分の面積を求める 置換積分のコツ uで置き換え (指数)× (三角関数)の積分のコツペアを作れ! stepⅡ: から までの総和を求める



面积公式大全小学数学必背公式全集 面积计算




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



三角形面积计算公式 三角形面积计算的万能公式 最全知识分享



非直角三角形的面积




17 空間向量的外積平行四邊形的面積推導 Youtube




计鹏视角 固定式光伏方阵占地面积计算方法 太阳能电动汽车网



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



三角形面积公式sin 万图壁纸网



Bmaplib Geoutils计算多边形面积bug调试记录 Junior2ran S Island




橢圓面積證明法 心中的科學 科學的探索 探索的心中 隨意窩xuite日誌




三角形的面積



常用图形求面积计算公式 瑞达电器资料网 华玉生活



正三角形面積公式



三角形面积公式 快懂百科



三角形面积的计算公式 信息阅读欣赏 信息村 K0w0m Com




定积分求y1 Sin5x与y2 Sin7x围成的面积 百度经验
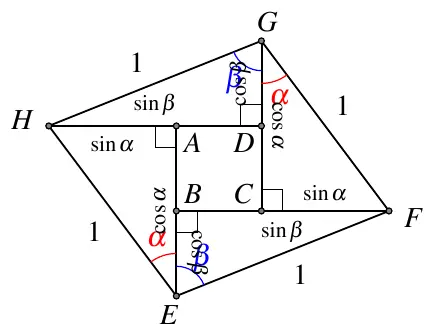



两角和差的正余弦公式的若干证明方法 如鱼饮水




四边形面积




圓周長計算圓形周長計算器 Frlvm




两圆相交面积 两个圆相交处的面积怎么计算 三人行教育网 Www 3rxing Org
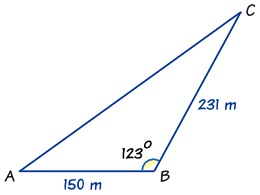



非直角三角形的面积
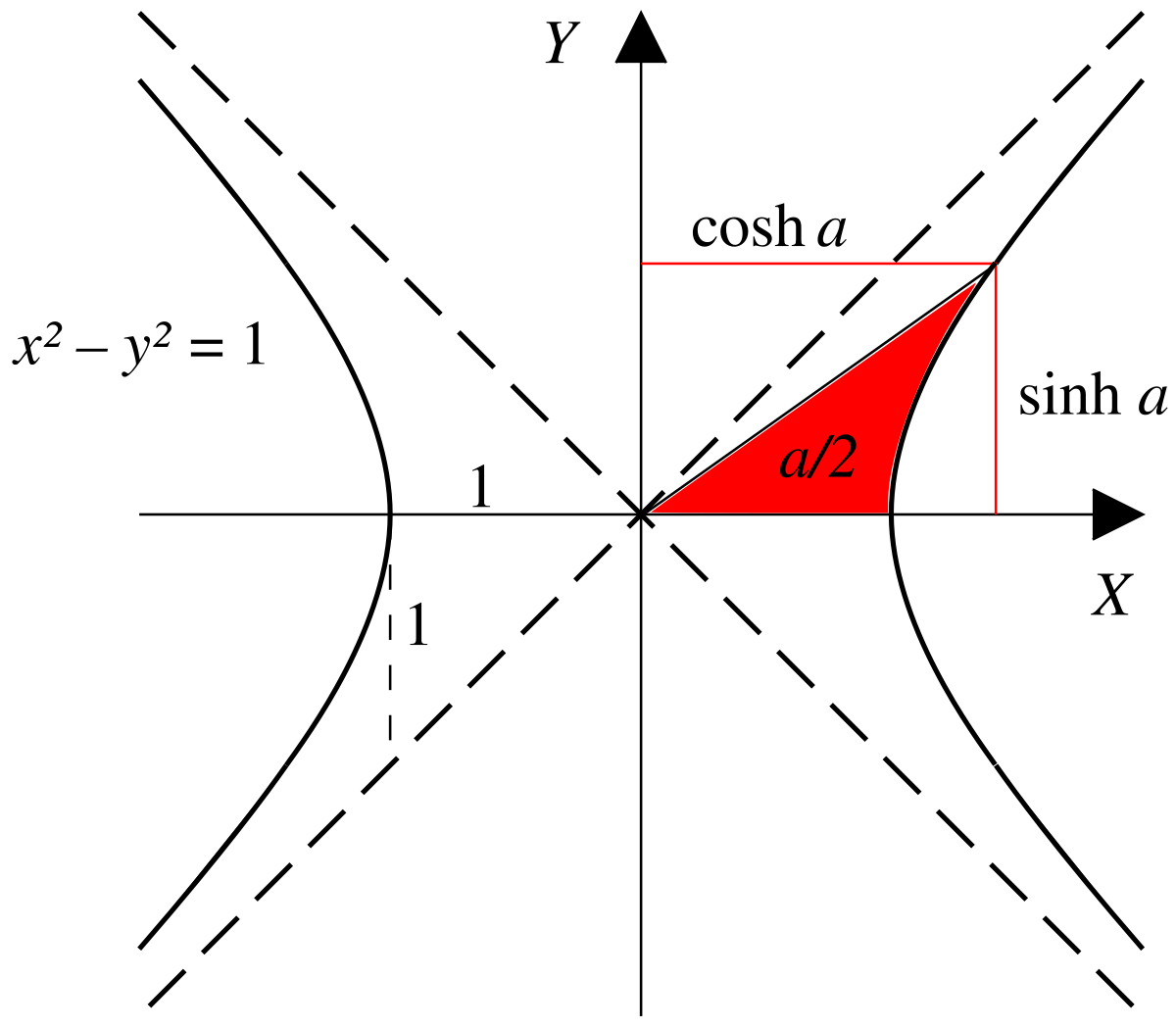



双曲函数 维基百科 自由的百科全书




Amc系列 第一講 數學中的面積公式都是怎麼來的 每日頭條




月形面积 弧长 弦长 弦高 周长 圆心角计算公式与在线计算器 三贝计算网 23bei Com




怎么看三角形投影 三角形投影面积如何计算 三人行教育网 Www 3rxing Org




三角形的面積
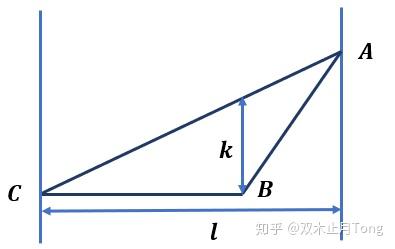



国际数学竞赛 三角形面积公式知多少 知乎




怎么计算三角形面积 生活百科




球冠体积公式 球冠体积公式



1




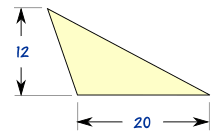
4种方法来计算三角形面积




正在計算界定面積
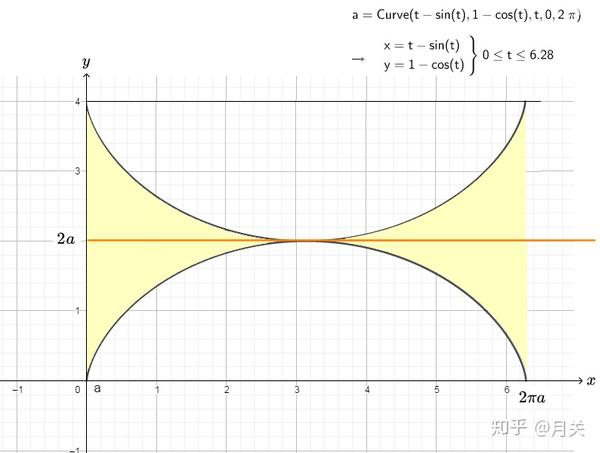



摆线的面积公式是什么 由摆线和x轴围成的图形绕某个直线所产生的旋转体体积如何计算 摆线与x轴的面积




三角形面積公式sin 三角形面積公式 Duph



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积



三角形面积公式sin 万图壁纸网



三角形面积用sin表示 三角形的面积公式sin 解三角形三角形面积




三角形面积计算公式 三角形面积计算的万能公式 52fmz购物网



少有人走的路 三角函数超入门 4 钝角三角比 三角形面积




3 10 三角形面積公式的推導 Youtube



用向量算面積 老王的夢田 痞客邦




平行四边形的面积公式对角线乘积的一半推导 计算机器在线计算



非直角三角形的面积




屋顶计算 如何计算屋顶的倾斜角度 The的长度和屋顶材料的面积



三角形面积公式是什么 三角形面积计算公式计算大全 Win7系统之家




三角形公式面積三角形面積公式 Utvos



椭圆面积计算公式 椭圆面积计算公式画法



定积分计算例题及过程 巩固基本概念 定积分验证计算2 学习岛




如何计算等腰三角形的面积 包含图片




那些你不知道的技巧 四邊形分割後面積計算 Dsemathinfo




三角形面积的计算公式 Sumyblog



三角形面積公式小學




怎么计算三角形面积 生活百科




怎么计算三角形面积 生活百科




體積計算公式體積公式 百度百科 Mrsysy




怎么计算三角形面积 生活百科




圆扇形与弓形




双曲函数 维基百科 自由的百科全书



三角形面积的计算公式 信息阅读欣赏 信息村 K0w0m Com




三角形的面積




如何计算函数y1 Cos3x与y2 Sin3x 5围成的面积 百度经验




三角形面积公式sin计算公式推导过程详解说明 计算机器在线计算



数理之路 三角形面积公式以及三角函数正弦和角公式 腾讯新闻




Sin Cos Tan公式sin Yzkgo




三角形的面積




Amc系列 第一講 數學中的面積公式都是怎麼來的 每日頭條




4种方法来求四边形的面积




4种方法来计算三角形面积




正在計算界定面積



如何计算y1 Sin2x与y2 Sinx 4围成的面积计算 函数



兩圓重疊面積計算 輸入數值自動計算 Lazyorangelife




利用正弦計算三角形面積 Finding Area Of A Triangle By Sine Ratio Youtube
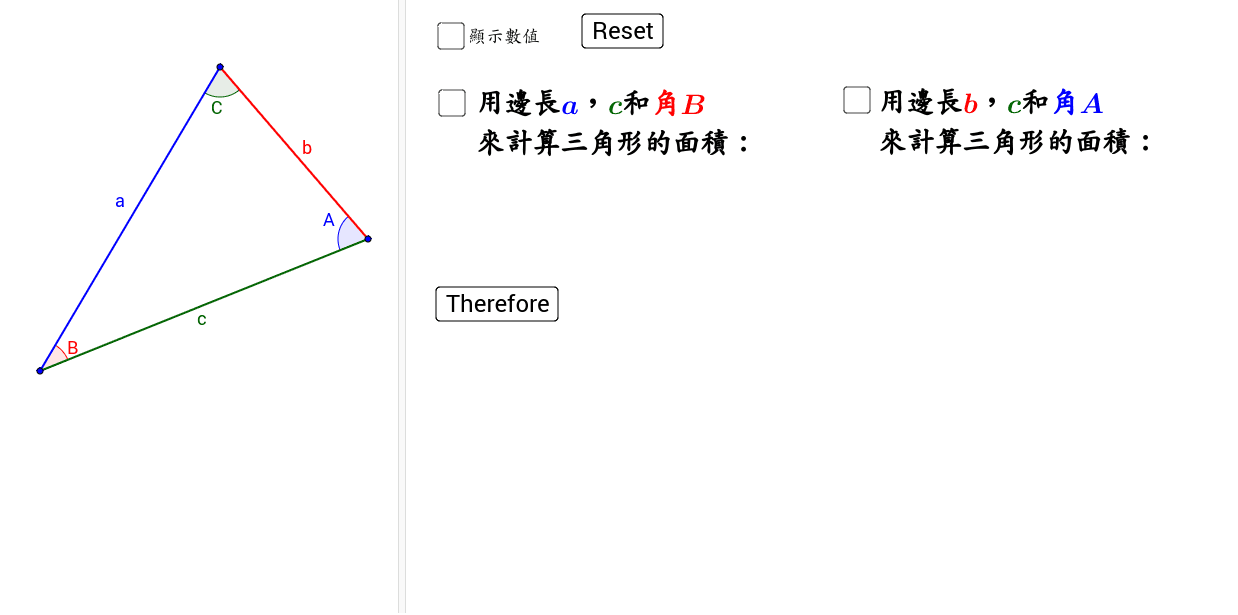



Proof Of Sin Formula正弦公式的證明 Geogebra




三角形面積公式 兩邊一夾角 Youtube




计鹏视角 固定式光伏方阵占地面积计算方法 太阳能电动汽车网




Arcgis风暴 Arcgis10 6图斑椭球面积计算原理与方法 刘一哥与gis的故事 程序员宅基地 椭球面积 程序员宅基地




3种方法来计算菱形的面积



初三数学 如何计算sin75 其实并没有你想想的那么复杂 哔哩哔哩 Bilibili
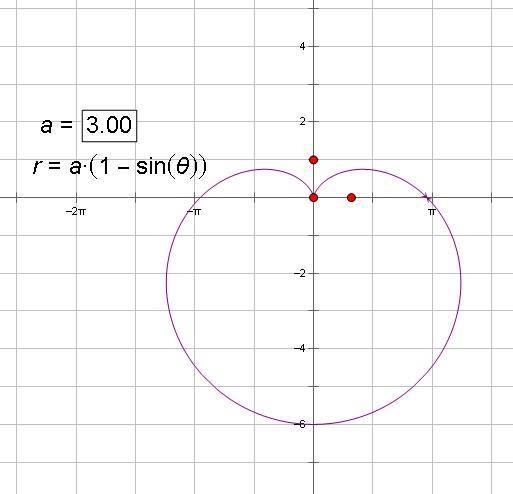



极坐标系的一元积分计算笛卡尔心形线面积 心形线的面积求解过程 桃丽网




干货详解spwm波等效面积计算法 电源网



三角形面积公式sin 万图壁纸网
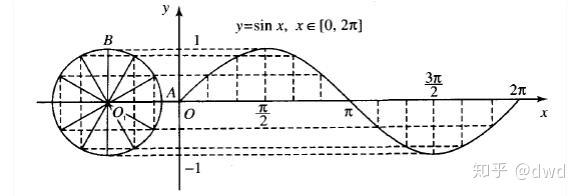



N维空间微积分微元 N维最大填充密度x Sin Nx 计算公式 知乎




學測數學 不用再怕 三角函數相關公式一把抓 Clear筆記共享 學生愛用app 痞客邦




Knowledge Teaching 圓形 缺角圓形面積計算 Area Calculation Of Circle Cutting Area Circle




Cad面積換算area 面積計算 Qaxnl




利用sin計算三角形面積 Teaching For Kn 我們一起來分享我們的數學 Youtube




淺談 三角形面積公式 Hackmd




对面积的曲面积分 Jason S Blog




关于python 计算四边形的面积 码农家园




三角形面积公式 三角形面积公式盘点 52fmz购物网




三角形面積公式 三角形面積公式是指使用算式計算出三角形的面積 同一平面內 百科知識中文網



0 件のコメント:
コメントを投稿